The Culver Twist Formula
The equations
The Culver equation is formulated to provide a twist distribution which provides a very close approximation to the optimum span loading. In sum, increasing the coefficient of lift near the center line of the wing reduces the necessary down force generated by the wing tips. If you can mold the lift distribution to a more elliptical shape, the induced drag is reduced.
Interestingly, getting the lift
distribution close to the ideal elliptical shape requires several
control points. Two control points, root and tip, is obviously
insufficient for the task, but many control points would make for
difficult and time consuming construction. Irv was able to minimize the
number of points at three - one at the root, one at the tip, and the
third at a point 0.3 of the semi-span out from the center line. Most
wings can thus be fashioned with three tamplates when using the foam
core method.
- CLD, design coefficient of lift:
- The greater the design coefficient of lift, the more wing twist will be required. The design coefficient should be chosen as described above.
- AR, aspect ratio:
- The aspect ratio of the complete wing.
- §¡:
- The sweep angle of the wing in degrees as measured at the half chord line.
- a¡RT:
- Total twist angle of the zero lift lines from root to tip.
- a¡S:
- The angle of the zero lift line at any station relative to the tip (1.0) in degrees.
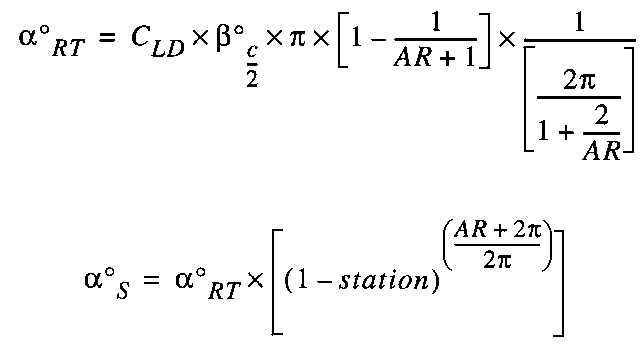
A few caveats and suggestions are in order:
(1) Do not invert airfoils. Use sections with forward camber and low pitching moments.
(2) Twist angles from the formula are always denoted relative to the zero lift angle.
(3) Contrary to the Panknin formula, in which the design
coefficient of lift is usually that at cruise, Irv's formula is based
on a coefficient of lift between 0.8 and 1.4. Use 0.8 if high speed is
the only goal. Coefficients of lift of 1.0 to 1.2 should be used for
high performance thermal machines.
(4) The elevons to be used are
of tapered planform. At the wing tip, the elevon can be up to 50% of
the chord, tapering down to a zero percent chord at around 40% of the
semi-span. This allows good thermalling with the elevons in trail, and
high speed flight is accomplished using a minimal amount of down trim.
Spreadsheets
- Aaron Coffey has written an Excel spreadsheet to calculate the required geometric twist when using the Culver twist distribution.
links page for conventional aircraft
links page for tailless aircraft
plotters and helpers main page
B2Streamlines home page.